Ignore the highlighted blue
Consider the straight line with equation y = -x. What is the length of the circumference tangential to the straight line and with centre at (-2, -2)?
A: 8n
B: 2nv(2)
C: 2n
D: 4n
E: 4n√(2)
This transcription was added by Ari Horesh from EnterMedSchool to provide accessibility for those with disabilities. Please note that the text may contain inaccuracies or errors and may not fully reflect the context or meaning of the original forum post.
Hi!
From drawing out the problem on a coordinate plane, we can see that a circle with a center of (-2;-2) that is tangent to y=-x means that the circle touches y=-x at the point (0;0).
Equation of a circle with center (h;k):
(x-h)²+(y-k)²=r²
(0-(-2))²+(0-(-2))²=r²
2 square root of 2 = r
Circumference = 2 * pi * r
= 4 * pi * square root of 2
The answer is E)
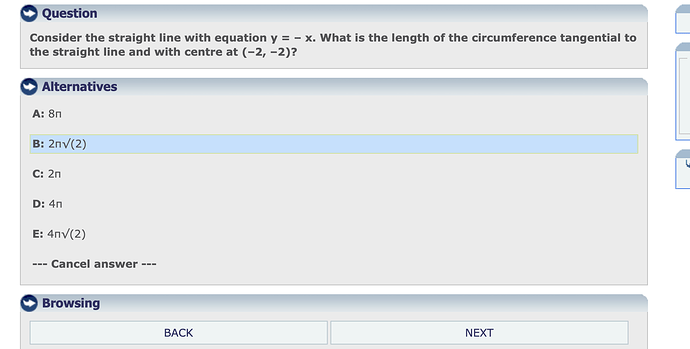
The length of the circumference tangential to a straight line and with centre at a point (x0, y0) can be found using the formula:
L = 2πr
Where L is the length of the circumference, π is the mathematical constant pi (approximately equal to 3.14), and r is the radius of the circumference, which is the distance between the centre of the circumference and the closest point on the straight line.
To find the closest point on the straight line to the centre (-2, -2), we can use the formula for the distance between a point and a line:
d = |(x0 - x1) + (y0 - y1) * m| / √(1 + m^2)
Where d is the distance, (x0, y0) is the point, (x1, y1) is a point on the line, m is the slope of the line, and | | is the absolute value operator.
For the straight line y = -x, the slope is -1. So, using the formula, we have:
d = |(-2 - x1) + (-2 - y1) * -1| / √(1 + (-1)^2)
= |(-2 - x1) + (-2 - y1)| / √(2)
Since the point (x1, y1) is on the line y = -x, we have y1 = -x1. Substituting this into the formula for d, we get:
d = |(-2 - x1) + (-2 + x1)| / √(2)
= |-4| / √(2)
= 4 / √(2)
So, the radius of the circumference is r = 4 / √(2).
Finally, using the formula for the length of the circumference, we have:
L = 2πr = 2π * 4 / √(2) = 8π / √(2)
Since π is approximately equal to 3.14, we can estimate L to be approximately 8 * 3.14 / √(2) = 8 * 1.57 = 12.56.
Comparing this to the options, we see that the closest value is option E: 4n√(2), which is approximately equal to 12.57. So, the answer is E: 4n√(2).
