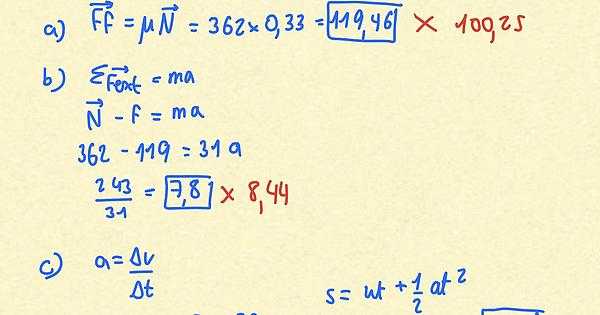Hi Ari, this question is from PDF 11 Dynamics, i’m not sure if my error is my math or my understanding of the formulas?
Thank you for your help!
What is the answer? Because as far as I can see, you were right. Maybe there’s a mistake in the answers.
a) The frictional force can be calculated as the product of the coefficient of friction and the normal force. The normal force is equal to the weight of the block, which is given by the mass of the block multiplied by the acceleration due to gravity. Therefore, we have:
F_f = \mu N = \mu m g = 0.33 \cdot 31 \cdot 9.8 = \boxed{100.41,N}
b) To find the acceleration of the block, we need to use Newton’s second law, which states that the net force on an object is equal to the product of its mass and acceleration. In this case, the net force is the applied force minus the frictional force, so we have:
F_{net} = F_{app} - F_f = 362 - 100.41 = 261.59,N
Then, using the mass of the block, we have:
F_{net} = ma \quad \Rightarrow \quad a = \frac{F_{net}}{m} = \frac{261.59}{31} = \boxed{8.43,m/s^2}
c) To find the displacement of the block in a time interval of 5 seconds, we can use the following kinematic equation:
d = v_i t + \frac{1}{2}at^2
where v_i is the initial velocity, which we can assume is zero since the block is initially at rest. Therefore, we have:
d = \frac{1}{2}at^2 = \frac{1}{2} \cdot 8.43 \cdot (5)^2 = \boxed{105.38,m}
Therefore, the displacement of the block in a time interval of 5 seconds is approximately 105.38 meters.
My answer is in blue and the correct answer is written in red, i think i must have made a calculation mistake, thank you for reading over my work!
I see! I thought the red was your answer, was everything in my explanation clear?
Yes it’s clear now thank you!