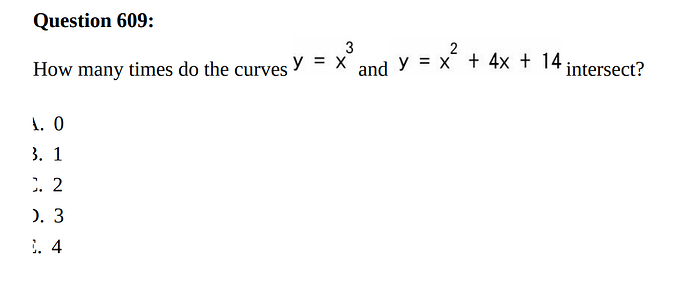I think its 3 points. Which is C
What I did was the following:
-
To find the how many times the lines intersect you should equate both equations together.
-
Equating them together gives us x^3=x^2+4x+14
-
Equate this to 0 so, x^3-x^2-4^x-14=0
This is a cubic which generally has 3 intersection points but it might not depending on the equation but you can factor out x and use the quadratic equation for the polynomial inside the bracket which in total gives us 3 points
To solve this you need knowledge of derivatives, local maximum and local minimum.
It’s not in IMAT’s syllabus.
Hi,
No need to do that. They have nothing to do with the intersection of graphs. They just represent the path of a single graph irrespective of the other graph.
Ahmadooo is mostly correct. As he says, you have to equate the two polynomials, simplify and the resulting 3rd degree polinomial is enough to show that you have three intersections. But you cannot factorize x out of this polynomial without deviding -14 to x which is unnecessary.
Intersection of graphs are actually part of IMAT syllabus!
Thank you for your response sir, I didn’t say that the intersection of graphs aren’t part of IMAT syllabus , I was referring to solving a cubic function which needs understanding of derivatives and critical points, is not part of it, the suggested way of solving this is based on the idea that a cubic function gives 3 answers, same way a square function should give 2 answers, but this answers should be checked to see if the y are real so the answer should be as the following:
f(x) = x^3 - x^2 - 4x - 14
f’(x) = 3x^2 - 2x - 4
This results in
X1= (1+(sqrt 13)/3) X2= (1-(sqrt 13)/3)
These are the critical points for this function
Now we need to determine the nature of these critical points so we use the points in the 2nd derivative of this function to find their nature
f’'(x) = 6x - 2
f’‘(X1) = 2 (sqrt 13) which is > 0
f’'(X2) = -2 (sqrt 13) which is < 0
This proves that X1 is a local min and X2 is a local max
With this knowledge and using some number such as x=0 , 1, 2 -1, -2 and graphing this function we can see this only has one real answer and only crosses the x axis once , by using the Desmos function Grapher or a cubic function solver , it will show that this function has only one rational answer.
EDIT:
I went on to read more about the cubic functions and graph intersections and by the use of Vieta’s Equivalents, I figured out when talking about intersections of graphs, we are interested in finding all the points of intersection, including all real and complex results, so this shows that this has 3 intersections.
which begs the question , so if we have a X^n function it should always intersect n times? correct?
Thank you for your reaction.
I am aware of your reminder of derivatives out of IMAT syllabus and it is correct what you wrote. My reminder about the intersections in the IMAT to emphasize and prevent an exchange with derivatives must have been inserted in a separate comment and not in a reply to you. Therefore I apologize for this technical issue.
Regarding the cubic function, I still do not understand what you should use its intersection with the x-axis for. Here, the question is about the intersection of the two graphs with one another and not the x-axis. Even if the question meant intersection with the x-axis, you just needed to solve the functions. As earlier wrote local min/max and pivotal points do not play any role in the functions continuity and its intersection.
You can look these up in the Calculus I & II by Adams et al. (University books)
Thank you.
About n’th degree, it is correct with n roots.
No need to involve complex roots/results.
thank you very much!!