IMAT 2012 Q11 [Paint]

Past Papers Solutions Archives
,
1

I wish to repaint the walls of my garage. It is 3 metres high, 4 metres wide and 9 metres deep. I shall not need to paint the electronic door which covers one 3 x 4 metre end, nor the window, which is 2 metres wide and 1 metre high, nor the rear door which is 1 metre wide and 2 metres high. 1 litre of paint covers 3 square metres.

How many 1 litre tins will be needed to complete the painting?

A. 26
B. 22
C. 25
D. 18
E. 21

2

Simple steps to solve word problems:

  • Underline key information
  • Determine what they are trying to ask, and what you will need to solve it
    1. Eliminate any non-essential information
  • Draw a picture, graph, or equation
    1. In moments of high stress like exam taking, always work with the paper they give you to avoid careless mistakes.
  • Solve.

This is a three step problem with one important subtlety; we cannot simply find the entire surface area, only the walls (not roof or floor). We need to calculate the surface area of the walls of the garage, subtract the areas we do not need to paint, and calculate the amount of paint needed.

  1. Finding the total surface area of the garage walls

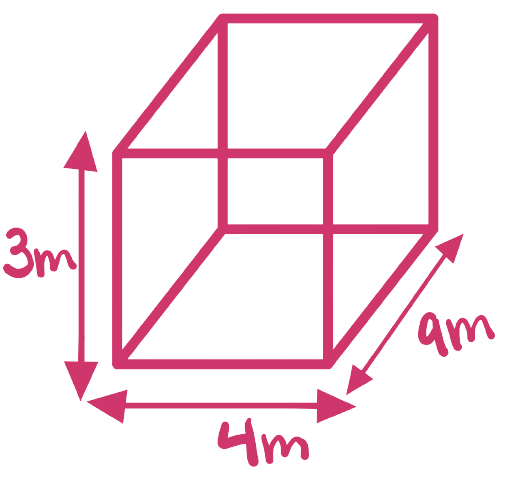
2(3m)(4m)+2(3m)(9m) = 78m

  1. Find the only the painted area

Unpainted area = (2m)(1m) + (3m)(4m) + (1m)(2m) = 16m

Total surface area - unpainted surface area = painted surface area

78m - 16m = 62m

  1. Find the amount of paint needed.
\frac{62m}{3m/L}
\fcolorbox{red}{grey!30}{21L}

We know that it’ll be a number bigger than 20 but less than 21. But you can only buy paint by the can, so we round up to 21. Therefore E is the answer.

2 Likes