Three identical capacitors are connected as follows:
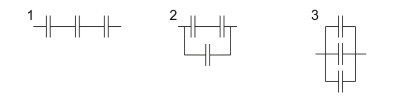
Which of the following shows the order of increasing capacitance (smallest first)?
A. 3, 2, 1
B. 1, 3, 2
C. 2, 1, 3
D. 1, 2, 3
E. 2, 3, 1
This is a simple, straightforward question. The only information you would need to know are 2 facts:
-
When connected in parallel, the capacitance of the capacitors is added:
^Ct= ^C1+^C2 +^C3 -
When connected in series, the capacitance of the capacitors is calculated by finding sum of the reciprocals inverted:
\frac{1}{^Cn} = \frac{1}{^C1}+ \frac{1}{^C2} + \frac{1}{^C3}
Therefore it is easy to conclude that the largest capacitance (for an identical number of identical capacitors) would be connected in parallel.
1 is connected in series, making it smallest. Between 2 and 3, 3 has more capacitors connected in parallel. So our ranking becomes 1-2-3, option D.
4 Likes