ABCDE is a regular pentagon. The transformation R is a rotation about the origin and maps A to B, B to C, C to D, etc. The transformation S is a reflection in the y-axis.
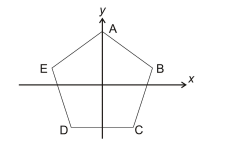
Which of the following sequences of transformations (performed in the order that they are listed) would NOT leave vertex D in the same position?
A. R R S R S R
B. S R
C. S R R S R S
D. R S R S
E. R S R R
The answer is A, sequence R R S R S R.
-
By undergoing R twice, we are at back at A.
-
By undergoing S, this leaves us still at A.
-
By undergoing R once again, we are now at B.
-
By undergoing S, we have completely left the pentagon and another R nor S can put us back on the pentagon respectively.
Therefore, A will not leave D at it’s start position.
2 Likes
I don’t think that the sequence “RR” brings us “back at A”; rather I think we’re with “A” at “C”. And now the vertical flip S makes what was “C” leave the original pentagon for good, a crime that could never be redressed :-). Hence, no further twisting and flipping will bring “D” to its original position and the answer is indeed (A).
