A novelty shop sells a rather unusual clock designed to puzzle users. There is only one hand, which points upwards. It has two faces. The larger hour face rotates clockwise and the smaller minute face rotates anticlockwise. Each face has one big dot, representing 12 o’ clock or 0/60 minutes and 11 smaller marks counting one hour or five minute divisions. There are no numbers.
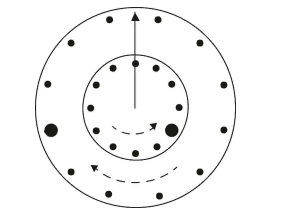
What time is it when the clock looks as shown in the diagram?
A. 9:20
B. 3:20
C. 8:40
D. 3:40
E. 8:20
Simple steps to solve word problems:
The first thing we want to do is identify which circle is which. We know that the large hour rotates clockwise, so it must be the outside circle. The inner circle is going anticlockwise so it must be the minutes. After we figure this out, we can count from the largest dot in the circles to the arrow that determines the hour and minute. This step is different in the outer and inner circles because we need to count in the appropriate direction, either clockwise or counterclockwise.
Let us start with the inside clock because there is a dot exactly on the arrow. We will count from the dot, anticlockwise, to the larger dot. In doing this, we count to 8. Note that this is the minute’s hand, so to find the time in minutes, we need to multiple (8)(5) = 40min. We do this subconsciously when we read a clock in real life.
Based on this one step we can eliminate 3/5 answers.
Next, to find the hours, we will do the same thing but in the opposite direction. Note that we start counting on the point to the right of the arrow because the dots pass the arrows moving left to right (clockwise). If we count from here, we count to “8”.
