A uniform beam, 3.0m long, of weight 100N has a 300N weight placed 0.50m from one end. The beam is suspended by a string 1.0m from the same end.
A diagram of the weights placed on the beam is given below:
How far from the other end must a weight of 80N be placed for the beam to be balanced?
A. 0.75m
B. 2.25m
C. 1.25m
D. 1.875m
E. 0.125m
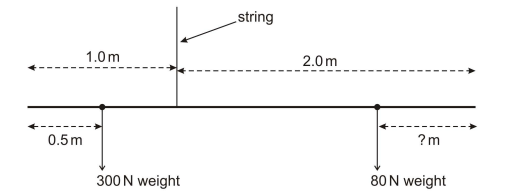
When solving moments, it’s imperative to know that in order for any beam to be in equilibrium, balanced or uniform; the anticlockwise moment must be equal to the clockwise moment.
A second piece of information to always look out for is whether the weight of the beam is taken into account. You can see in this question it is, therefore, the weight of the beam will also have a moment.
We can tell by looking at our system that:
The Anti-Clockwise moment is the system between the 300N weight and distance 0.50m from the end of the beam.
The clockwise moment is the system between the 80N weight and our unknown distance x. But don’t forget, the weight of the beam also accounts for the clockwise moment. This means that for the clockwise moment, we must calculate 2 sets of values and add them to give us the final clockwise moment.
We can make our simplest calculation first:
A moment (M) in Newton meters is equal to the product of the Force (F) in Newtons and the perpendicular distance from the pivot (d) in meters.
M=Fd
With the provided values we are able to deduce the Anti-clockwise moment.
M_{AC}= F \times d= 300N \times (0.5 m) = 150 Nm
Now, the only way we will be able to solve the clockwise moment, which looks like this:
[Moment of weight of beam] M_{C1}= F \times d= 100N \times (0.5 m) = 50 Nm
[Moment of 80N weight] M_{C2}= F \times d= 80N \times ( 2-x) = [160-80x] Nm
[Total Clockwise Moment] M_{CT}= M_{C1} + M_{C2} = 50 + [160-80x] = [210-80x]Nm
Would be to equate it to the anti-clockwise moment, since the beam is supposed to be balanced.
M_{AC}= M_{CT},
where M_{AC}= 150 Nm and M_{CT}= [210-80x]
So we can say
[210-80x]= 150 Nm
Finally, we solve for x: (our unknown distance)
150+80x= 210
80x= 210-150
80x=60
8x=6
x= 6\8
x= 3/4 m or 0.75 m
Making our answer A.