Simplify
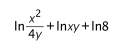
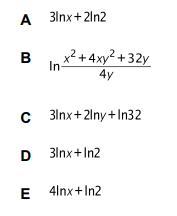
Simplify
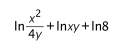
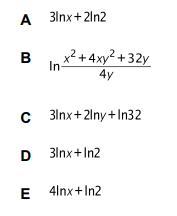
Using the Natural Logarithm laws:
p.s. \ln =\log _{e}
\ln\frac{x^2}{4y} + \ln xy + \ln8 = (\ln x^2 - \ln 4y )+ (\ln x + \ln y )+ \ln 2^3
= (2\ln x -(\ln 4 + \ln y)) + \ln x +\ln y + 3\ln 2 = 2\ln x - \ln 2^2 - \ln y + \ln x + \ln y + 3\ln 2
=3\ln x - 2\ln 2 +3\ln 2 \to 3\ln x + \ln 2.
Which is the answer to the question. (D)
If more explanation is needed, please ask me further. I tried to simplify it as much as i could.