The diagram shows a quarter of a circle surrounded by an isosceles triangle.
The radius of the circle is r.
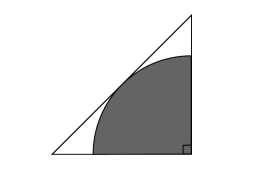
Which one of the following expressions represents the unshaded area?
1 Like
There are multiple ways to solve this question. I will type out the one that seems the easiest to understand.
Looking at the things added to the area, we can tell that the triangle is actually half of the square (divided diagonally). For a square, it is known that the value of diagonal of the square is a\sqrt2 where a is the value of one of the sides of the square.
Having this in mind, we have half of the diagonal as r, so we can make a simple equation: \frac{a\sqrt2}{2}=r \to a\sqrt2= 2r \to a = \frac{2r}{\sqrt2} \to a =r\sqrt2
As the triangle is half of the area of a square, we can calculate its area very easily now: P_t=\frac{a^2}{2}=\frac{(r\sqrt2)^2}{2}= \frac{2r^2}{2} \to P_t=r^2.
The area of a circle is calculated by the formula: \pi r^2
In this task, we have one forth of a circle, which area is one forth of the whole circle area: P_c=\frac{\pi r^2}{4}
In order to calculate the area of the unshaded area, we are going to subtract the quarter of the circle from the triangle area:
P = P_t -P_c = r^2 - \frac{\pi r^2}{4} =r^2 (1-\frac{\pi}{4}).
Which means that (A) is the correct answer.
3 Likes