15 runners took part in this year’s Marathon of Marathons (eight marathon races on consecutive days). Points were awarded to the first seven to finish in each race, as follows:
All 15 runners finished in the first three at least once, but only Philip, who was the overall winner with a total of 61 points, finished in the first three every time.
How many of the eight races did Philip win?
A. 2
B. 3
C. 5
D. 4
E. 1
Simple steps to solve word problems:
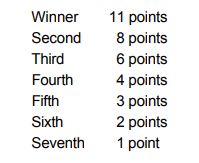
First, let’s sort out what is important. There are 8 races, Philip finished in the top 3 every race, and as a result he gets either 11 , 8 , or 6 points a race. He finishes with a total of 61 points, so we need to figure out a combination of the first, second, and third place points that will equal 61 over 8 races. The rest of the information is distracting, we don’t need to know the number of other runners, whether or not they finished in the two three, etc…
Approach: Find the maximum number of points he could have gotten and then adjust from there.
(8 races)(11 points per race) = 88 points
This is way to high so we would expect him to have won maybe closer to half of his races. We cannot know for sure but from here on out we need to guess and check. The only prediction we can make from this initial calculation is that our final answer will be a lot less than 8 wins.
If he won half his races:
(4 races)(11 points) = 44
Can we now find a way to make 61 - 44 = 17 from 8 or 6 per race for 4 races?
No we cannot, because even the minimum amount per race left (6 points), we are still way over with 24 points. Therefore we know he won even less than 4 races.
Let’s try 2 races won because we know it is less than 4 but we need an answer greater than 0. So 2 is our middle number.
(2 races)(11 points) = 22 points
So we need to find a way to make 61 - 22 = 39 from 8 or 6 per race for 6 races
This is mainly trial and error so let’s see if 6 per race left is enough.
(6 races)(6 points) = 36 points
Right away we can see this will not work because we will not be able to get 39 with only 6 and 8.
What if Philip won 3 races?
(3 races)(11 points) = 33 points
So we need to find a way to make $61 - 33 = 28 from 8 or 6 per race for 5 races, but again, this is too much! Even at 6 points per race for 5 races you finish with 30 points, not 33 (and if he came 2 nd with 8 points for any race here, he would still be off.
So by process of elimination we know the answer must be he won 1 race, but let’s show the math.
(1 races)(11 points) = 11 points
So we need to find a way to make 61 - 11 = 50 from 8 or 6 per race for 7 races
(7 races)(6 points) = 42 points, meaning we are 8 points off. To get 8 more points, you would have to come second 4 times.
So your final breakdown of points:
(1 races)(11 points) + (3 races)(6 points) + (4 races)(8 points)
11 + 18 + 32 = 61
Note that the solution is way too much for what you need. This was an attempt to show you what you should be thinking, but realistically you could solve half of this in your head and with scribbles on a piece of work paper. Do not feel overwhelmed with seeing a longer overcomplicated solution.