The table below shows the average mass of the cerebellum, which is a part of the brain, and total body mass, for a number of animal species. The cerebellum of a cat has an average mass of 5.3 g, while a cat’s average body mass is 3.5 kg.
For which of the species shown is the ratio of cerebellum to total body mass closest to that of the cat?
A. Pigeon
B. Squirrel
C. Dog
D. Rabbit
E. Mouse
Simple steps to solve word problems:
DO NOT BE AFRAID TO APPROXIMATE HERE!
This is not a hard question conceptually, but without a calculator, it can be difficult to tackle. Remember that we are working with ratios, so we can multiply or divide both sides of the ratios and it will still be a valid ratio.
First, let’s convert the cat’s mass to grams to make this easier:
3.5kg = 3500g
Brain : Body
5.3g : 3500g
Now, let’s take our options and try to get them to a similar range (in the low thousands). Let’s see what I mean by this:
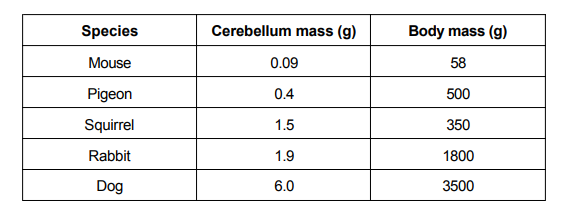
Mouse
100 (0.09g) = (58g) 100
9g = 5800g
Now let’s find a closer relationship with the cat, lets do this by multiplying the mouse ratio by 2 and the cat ratio by 3
Mouse
2(9g) = 2(5800g)
18g = 11600g
Cat
3(5.3g) : 3(3500g)
15.9g : 10500g
Close, but let’s keep looking:
Pigeon
10 (0.4g) = (500g) 10
4g : 5000g
Compared to the cat, it is much too small, smaller brain size and a bigger body in this ratio. We can eliminate this option.
Squirrel
10 (1.5g) = (350g) 10
15g : 3500g
This ratio is much too big, we have the same weight but a much larger brain. Therefore we can eliminate this option.
Rabbit
2 (1.9g) = (1800g) 2
3.8g : 3600g
We can eliminate this option because it is not as close as the dog ratio is to the cat ratio.
Dog
6.0g = 3500g
This is extremely close.
We can narrow it down to between the mouse and dog.
Refresh your memory:
Mouse
2(9g) = 2(5800g)
18g = 11600g
Cat
3(5.3g) : 3(3500g)
15.9g : 10500g
If we put the dog on the same scale:
Dog
6.0g = 3500g
3(6.0g = 3(3500g)
18g = 10500g
Notice how the cat and dog have the same body weight, and the mouse and the dog have the same brain weight at these ratios?
Therefore we can conclude that the mouse is more similar to the cat ratio. The mouse has a higher brain mass and a higher body mass than the cat when comparing these two ratios, so when it decreases, it will have a brain mass and a body mass which are smaller and more closer to the cat. The dog here already has the same body mass as the cat in this ratio, but it has the same brain size. This means that a mouse with a smaller ratio will have a smaller brain than the dog at a comparable size, which is closer to the brain size of the cat.
As a result, we can conclude that the answer is E, the mouse.
Proof using a calculator:
Take the ratio off all three animals:
Cat:
Dog:
Mouse:
Cat > Mouse > Dog
Mouse and cat have the closest cerebellum to body mass ratio.