Given that 2 log_{10} (x) – 3 = log_{10} (y)
Express y in terms of x.
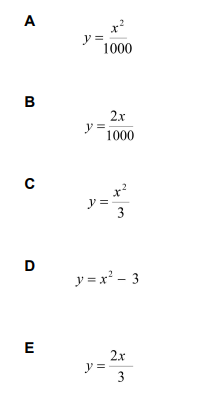
Given that 2 log_{10} (x) – 3 = log_{10} (y)
Express y in terms of x.
In order to solve this, we need to know some rules of the logarithm:
There are multiple ways to solve 2\log _{10}(x) -3 = \log _{10}(y).
I will solve it in one way that I think is the fastest (using rule 3 and 8):
2\log _{10}(x) -3 = \log _{10}(y) \to (rule 3)\log _{10}(x^2) -3 = \log _{10}(y)
\to (using 10^{function}) 10^{\log _{10}(x^2) -3} = 10^{\log _{10}(y)} \to 10^{\log _{10}(x^2)} \cdot 10^{-3}= 10^{\log _{10}(y)}
\to (rule 8) (x^2)\cdot 10^{-3} = (y) \to y = \frac{x^2}{10^3} \to y= \frac{x^2}{1000}
Which gives us the correct answer (A)
Hi,
I don’t get this part, how do separate the -3 ?
Is it like an exponent rule?
I found these two relevant rules:
a^m+n = a^m * a^n
a^m-n = a^m / a^n
but in this case, the 3 is negative, so we would have to divide 10^log10(x^2) by 10^log10(-3)
not multiply???
hello! this -3 is seperate from logx2 in the first place.
then we take the 10th power of both sides and include logx2 -3 in a panathesis
we open up the 10th power and write it as 10^logx2 * 10^-3 (normal exponential rule)
then solve it with the 8th rule
here you can see it from my solution a bit more clearly
Thank you so much! That really clears it up