The diagram shows a car of mass 1000 kg travelling at a constant speed of 30 m/s in the direction shown along a flat, level road which forms a circle of radius 50 m.
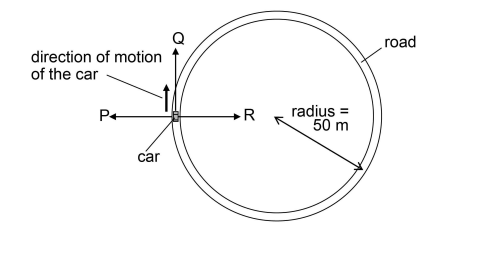
Which row in the table gives both the magnitude of the resultant force on the car and the direction of the acceleration of the car at the instant shown?
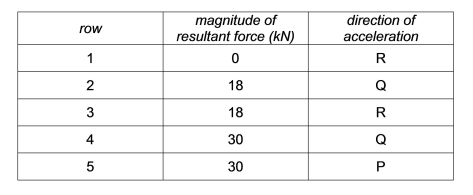
A. row 1
B. row 2
C. row 5
D. row 3
E. row 4
1 Like
This question revolves around understanding Centripetal Force.
“A centripetal force is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path.”
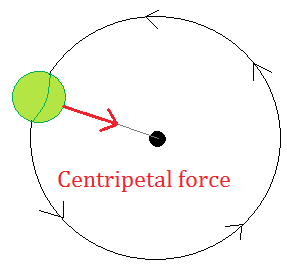
Since the direction of the force is always towards the fixed point of the instantaneous center of curvature of path, we can confidently say that is direction R. Centripetal force causes centripetal acceleration. (Remember: An objects accelerates in the direction of it’s resultant force: F=ma) Therefore we can say the direction of acceleration, the direction of force is also R.
Our answer is now narrowed down to 2 choices, row 1 or row 3, A or D.
The final step is to use the given information to actually calculate the resultant centripetal force. The formula for that being:
F_c= \frac{mv^2}{r}, where
F_c= Centripetal Force (N)
m= mass (kg)
v= velocity (m/s)
r= radius (m)
Therefore,
F_c= \frac{(1000)(30^2)}{50}= \frac{(1000)(900)}{50}= \frac{900,000}{50}= 18,000 N
Notice a small trick in the table, where they’ve listed the force in kN.
1000N= 1 kN
Therefore 18,000N= 18 kN
Our answer is Row 3, D.
10 Likes



