Given that
log_{10} ^7 = x
log_{10}^2 = y
log_{10}^3 = z
What is log_{10}(\frac{14}{3}) expressed in terms of x, y, and z ?
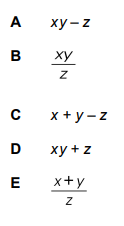
Given that
log_{10} ^7 = x
log_{10}^2 = y
log_{10}^3 = z
What is log_{10}(\frac{14}{3}) expressed in terms of x, y, and z ?
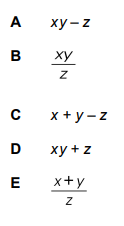
There are some rules for the logarithm that need to be remembered. These rules are:
So in order to solve the question, we will use these rules. In this particular situation we will use the rules 1 and 2.
\log _{10}\frac{14}{3} = \log _{10}14 - \log _{10}3 (using rule 2) \to \log _{10}(7\cdot2) - \log _{10}3 = \log _{10}7 + \log _{10}2 - \log _{10}3 (using rule 1) \to \log _{10}7 + \log _{10}2 - \log _{10}3 = x + y - z
Which finally gives us the solution to the question.