Simple steps to solve word problems:
- Underline key information
- Determine what they are trying to ask, and what you will need to solve it
- Eliminate any non-essential information
- Draw a picture, graph, or equation
- In moments of high stress like exam taking, always work with the paper they give you to avoid careless mistakes.
- Solve.
The most difficult thing in this problem is making sense of all the information they give us. We are looking for the DIFFERENCE in the price of buying discounted packs versus non-discounted. To do this, calculate the cost of just buying only single packs, and then solve for trying to find the cheapest combinations.
We know there is a set of triplets (3), a set of twins (2), and another single child (1). We want to find out how many crisps they have in a week (5 days since Mon-Fri) and they all have 1 each on those days. We also know they buy the chips monthly, which means there will be 4 weeks, each with 5 days they will have chips. So we are looking for 6 bags of chips per day for 20 days. (6)(20)=120.
Out of those 120, (3)(20) = 60 will be for the triplets, (2)(20) = 40 for the twins, and 20 will be for the last child.
Now we can start to piece things together and see the prices if we get multipacks. We know that the multipacks are one flavour and the triplets, twins, and the last child will all be getting different flavours.
Triplets (need 60)
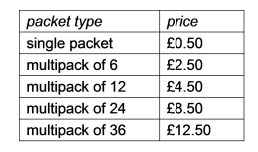
(1 multipack of 36) + (1 multipack of 24) = 60 total bags
(£12.50) + (£8.50) = (£21.00)
Twins (need 40)
(1 multipack of 36) + (4 single packets) = 40 total bags
(£12.50) + (4)(£0.50) = (£14.50)
Single child (need 20)
(1 multipack of 24) = (£8.50) but lets check another combination.
(1 multipack of 12) + (1 multipack of 6)+ (2 single packets) = 20 total bags
(£4.50) + (£2.50) + (2)(£0.50) = (£8.00)
The second option here is the cheapest, so be careful on exam day as they can be tricky like this.
Total cost of everything = £21.00 + £14.50 + £8.00 = £43.50
What if they bought only single packs?
(£0.50)(120 packs) = £60.00
Price difference = £60.00 - £43.50 = £16.50
\fcolorbox{red}{grey!30}{Therefore the answer is E, $£16.50$}