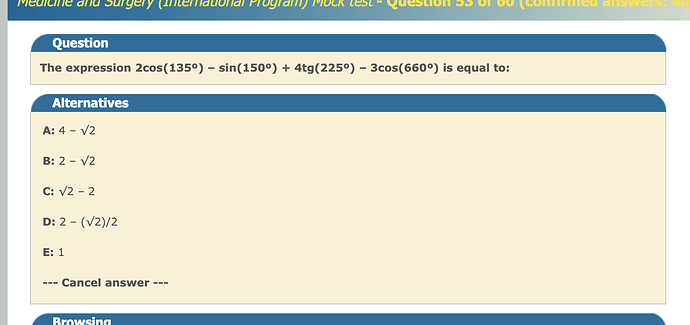
The expression 2cos(135°) – sin(150°) + 4tg(225°) – 3cos(660°) is equal to:
Alternatives
A: 4 - √2
B: 2 - √2
C: √2 - 2
D: 2 - (√2)/2
E: 1
Hi!
I used x° * pi/180 = x rad, as well as the trigonometric circle properties
2cos(135°)-sin(150°)+4tan(225°)-3cos(660°)
= 2cos(3pi/4)-sin(5pi/6)+4tan(5pi/4)-3cos(11pi/3)
= 2cos(-5pi/4)-sin(-7pi/6)+4tan(pi/4)-3cos(2pi/3)
= 2cos(-pi/4)-sin(-pi/6)+4tan(pi/4)-3cos(-pi/3)
= 2 * -square root of 2/2 -1/2 + 4 * 1 - 3 *1/2
= 2 - square root of 2
@AriHoresh i couldn’t find the correct answer when using the formulas -sin(x)=sin(-x) and cos(-x)=cos(x), does that mean they are incorrect?
Also, is this in the math syllabus?
Thank you!
I couldn’t see similar questions in the IMAT’s syllabus, only the BMAT’s and these questions got excluded as well over the years.
2 Likes